<問題>リンゴ1個とミカン1個合わせて320円です。ミカン1個の代金はリンゴの60%です。
ミカンとリンゴの代金を求めよ。
<ポイント>割合の問題を解くには、何が「もとにする量」で、何が「くらべる量」かをはっきりさせることです。この問題では、くらべる量が二種類あるので注意してください。
「もとにする量」や「くらべる量」をさがすには、「割合」の意味を考えることです。
この問題では、「ミカン1個の代金は、リンゴの60%」となっています。
「60%」とは、「もとにする量に対するくらべる量の割合が60%」という意味です。
言葉の順序を少し入れかえると、「くらべる量の割合は、もとにする量の60%」と言えます。
ここで、「リンゴの60%」という表現が「もとにする量」を発見する手がかりになります。
この部分は、「 〜 の 割合」という語順になっています。割合の問題でよく見かける表現部分です。
「〜」というところにある量が「もとにする量」です。重要!
したがって、この場合は、「リンゴ」がもとにする量になります。つまり「リンゴの代金」がもとにする量です。
「リンゴの代金」がもとにする量とわかれば、「ミカンの代金」は「くらべる量」となります。
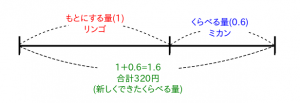
では、図で考えてみます。もとにする量は「1」として表します。60%=0.6です。
リンゴやミカンの代金を求めるためには、それらの代金をさがす手がかりが必要になります。それが、「新しくできた、くらべる量」の合計金額320円です。
合計金額320円の割合は、もとにする量をリンゴとすると1.6(160%)になります。
ここで、「く・も・わ」を利用します。
く:くらべる量
も:もとにする量
わ:割合
く = も × わ
も = く ÷ わ
わ = く ÷ も
320 ÷ 1.6 = 200 …リンゴの代金
なので、リンゴは200円となります。
それは、320が「くらべる量」、1.6が「割合」なので、「く・も・わ」の式から「く÷わ=も」となるからです。
リンゴの代金が200円だとわかれば、ミカンは320円から200円を引けば求められますね。
320 − 200 = 120 …ミカンの代金
または、
200 × 0.6 = 120
(リンゴの60%より、「のがけ」=[「の」をかけ算]を利用。200の0.6→200×0.6)
答 リンゴ:200円、ミカン:120円