文字(変数)の便利な点は、勝手に、好きなように定義(きまり・約束)を作ることができるところかな。もっというと好きなものを自分が定義した文字(変数)の中に放り込むことができるってことです。
1.文字(変数)とは
まるで、
文字(変数)は箱のような入れ物
です。
その中には、数や文字、文字式(文字を含む式)などを入れることができます。
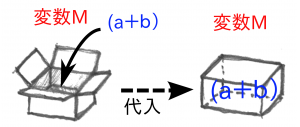
図1では、文字(変数)Mの中に(a+b)を入れています。(変数に数字や文字、文字式を入れることを代入という。)
もう一つ例、図2を見てください。
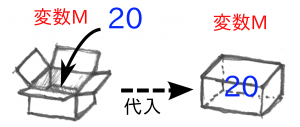
今度は、文字(変数)Mの中に20を代入しています。
このように、文字(変数)には、なんでも入れることができます。
例えば、人の身長を$x$cm、その人の年齢を$y$才なんてね。すると、$x$には、123cmとか189cm、$y$には、18才とか54才とかね。好き勝手に文字(変数)に入れられますね。だからといって、でたらめに入れることはできません。例えば、$x$には年齢は入れることができません。なぜなら、$x$は身長(cm)と約束(定義)しているからです。だから、$x$には1mなど単位がcmでないものも、入れることができません。つまり、一度、文字(変数)に入れるものを約束(定義)すると、それにしばられるのです。(ちょっと難しいですね。)
さらに、すごいのは計算にも使えるんだね。つまり、それを文字式という。さらに、等式にもなる。
例えば、リンゴ1個の値段を$x$円、個数を$y$個とし、その時の代金は、$xy$という文字式で表せます。また、代金を$z$とすると$z=xy$という関係が成り立ちます。$z=xy$は、等式と呼ばれます。
もしこれを、数字で表すと、リンゴ1個が128円(税込み)で、23個買った。その時の代金は、えっっと、あれ暗算では、ちょっと、電卓、電卓、、、、2994円となります。
文字式で表してみると、$xy$です。こちらの方が、簡単ですね。
中学生になっていちばん驚いたのが、円の面積の公式です。
小学校では、円の面積=半径×半径×3.14なので、半径が3cmの円の面積なら、3×3×3.14=28.26となり、半径が15cmなら…15×15×3.14=706.5となります。計算が、とても大変ですね。
しかし、中学校では、円の面積の公式は、$S=πr^{2}$です。rが半径です。
もし、半径が3cmなら、円の面積は、$3×3×π=9π$となり、半径が15cmなら、$15×15×π=225π$となります。
どうですか、とても簡単になりますね。私は、文字式を学習したとき、なんて便利なんだと感動したのを今でも新鮮に思い出します。
文字、文字式は、とても、便利な仕組みです。どんな所が便利かというと、計算をするときに式が複雑になる部分を1つの文字で置き換えて計算を進めることができる点です。面倒な部分を文字に置き換えると簡単に解決するのです。
もちろん、文字(変数)には、数字や文字(文字式)などを入れることもできますが、出すこともできます。
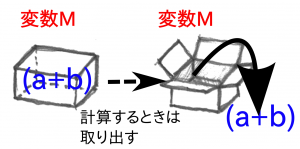
つまり、文字(変数)は、出し入れ自由な箱なのです。図3のように、計算のとき、計算の途中、計算の最後などいろいろな場所で、取り出すことができます。
2.式の展開に利用
さて、今回は、式の展開で、置換法を利用してみます。もちろん、文字の便利な点を最大限に活用します。
その前に、もう少し練習(前準備)します。
$(a+b)$を$M$とします。つまり、文字(変数)$M$の中には、$(a+b)$が入っているという考えです。($a+b$をカッコで囲んでいるのは、文字式をひとかたまりとしてあつかうことをイメージしています。)もし、$M^{2}$という文字式があったとします。それは、何を意味しているかというと、$(a+b)^{2}$を表しているのです。
【問1】$(a+b)(c+d)$を置換法を利用して解いてみます。\[まず、(c+d)をMとします。\tag{文字Mが変数で、その中に(c+d)を入れたと考えます。} \]\begin{align} &(a+b)(c+d) \nonumber \\ &=(a+b)M \tag{1} \\ &=aM+bM \tag{さらに、(1)の式を分配法則で、展開します。} \\ &=a(c+d)+b(c+d) \tag{Mの中に入っていた、(c+d)を外に出します。} \\ &=ac+ad+bc+bd \tag{分配法則で、すべて展開します。これが、式を展開したものです。} \end{align}
展開の答え:
$(a+b)(c+d)=ac+ad+bc+bd$
もう一度見てみると、文字(変数)Mの中には、(c+d)という文字式が入っているのです。
もう少し難しいものに挑戦してみましょう。
【問2】$(a+b+c)^{2}$を展開しなさい。
では、さっそく置換します。例えば、$(a+b)$をMとします。(もちろん、$(b+c)$をMとしてもいいです。お好みでどうぞ。)
\begin{align}&(a+b+c)^{2}\\&=(M+c)^{2}\\&=M^{2}+2Mc+c^{2}\\&=(a+b)^{2}+(a+b)c+c^{2}\tag{Mを(a+b)にもどしました。}\\&=a^{2}+2ab+b^{2}+ac+bc+c^{2}\end{align}
3.因数分解で利用
今度は、因数分解にチャレンジします。
【問3】$(x-2)^{2}-3(x-2)+2$を因数分解しなさい。
\begin{align}&(x-2)^{2}-3(x-2)+2\tag{(x-2)をMとする}\\&=M^{2}-3M+2\nonumber\\&=(M-2)(M-1)\tag{Mを(x-2)にもどす}\\&=((x-2)-2)((x-2)-1)\nonumber\\&=(x-4)(x-3)\tag{因数分解完了}\end{align}
【問4】$(x+y)^{2}-4$を因数分解しなさい。
\begin{align}&(x+y)^{2}-4\tag{(x+y)をMとする。}\\&=M^{2}-2^{2}\tag{4は$2^{2}$です。}\\&=(M+2)(M-2)\tag{Mを(x+y)にもどす。}\\&=((x+y)+2)((x+y)-2)\nonumber\\&=(x+y+2)(x+y-2)\tag{因数分解完了}\end{align}
4.おまけ
今度は、少し変わった利用の仕方です。基本的な考え方は今までと同じで面倒なところを文字に置き換えます。
【問5】$(3\sqrt{2 \ }-3)(3\sqrt{2 \ }-5)$を計算しなさい。この式を見て、特に何も感じない人はそのまま解いてください。少し抵抗を感じる人は次のように置換法を利用します。
\begin{align}&(3\sqrt{2 \ }-3)(3\sqrt{2 \ }-5)\tag{$3\sqrt{2 \ }$をMとする。}\\&=(M-3)(M-5)\nonumber\\&=M^{2 \ }-8M+15\tag{Mを$3\sqrt{2 \ }$にもどします。}\\&=(3\sqrt{2 \ })^{2}-8(3\sqrt{2 \ })+15\nonumber\\&=18-24\sqrt{2 \ }+15\nonumber\\&=-24\sqrt{2 \ }+33\nonumber\end{align}
【問6】百の位の数字をa、十の位の数字をb、一の位の数字をcとしたとき、この3けたの整数をa、b、cを使った式で表しなさい。
\begin{align}&3けたの整数の例として、342を考えます。\nonumber\\&342=3×100+4×10+2\tag{位の数字と整数の関係がわかるように式を組み立てる。}\\&\Longrightarrow a×100+b×10+c\tag{3をaに、4をbに、2をcに置換する。}\\&=100a+10b+c\tag{これが答えです。}\end{align}
こんなものもあります。ふつう、代入法とよばれていますが、置換法として考えても解けます。
【問7】次の連立方程式を代入法で解きなさい。
\begin{eqnarray} \left\{ \begin{array}{l} x = 7 – 3y \hspace{ 10pt }\cdots ①\nonumber\\ x – 2y = -3 \hspace{ 10pt }\cdots ②\nonumber \end{array} \right. \end{eqnarray}
このとき、$( 7 – 3y )$を$x$に、置換したと考えます。それが、①の式です。②の式に①の式を代入することを考えます。次のように表せます。
\begin{align}( 7 – 3y ) – 2y = -3\hspace{ 10pt }\cdots ③ \nonumber\end{align}
③の式は、置換した後の文字(変数)$x$から、中身の$( 7 – 3y )$を取り出したものであると考えます。つまり、連立方程式①、②は、置換と置換した文字を用いた式を表していると考え、式③で、置換した文字 $x$ から代入した値(式)$( 7 – 3y )$ を取り出していると考えることができます。
では、最後まで解いてみましょう。あとは、普通に解くだけす。式③から解き続けます。
\begin{align}( 7 – 3y ) – 2y &= -3\nonumber\\7 – 3y -2y &= -3\nonumber\\-5y &= -10\nonumber\\y &= 2\nonumber\\&y = 2 を、①に代入します。\nonumber\\x &= 7 – 3 × 2\nonumber\\x &= 1\nonumber\\&( x , y ) = ( 1 , 2 )\hspace{ 10pt }\cdots (答え)\nonumber\end{align}
いろんな場面で、置換法が利用できます。みなさんも、気づいたら教えてください。
以上で、置換法の実技を終了します。文字(変数)を上手に利用できることを祈っております。