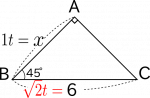$1:2:\sqrt{3}$や$1:1:\sqrt{2}$、$3:4:5$、$5:12:13$などの直角三角形の辺の比を利用した辺の長さを求める方法を紹介します。
一般的な辺の比の利用のし方は、次のようなものです。
<例1>下図の直角三角形で、$x$、$y$の長さを求めなさい。
- 図1:x、yの長さを求めなさい。
図1の直角三角形は、30゜、60゜の特別な直角三角形です。辺の比は、$BC:AB:AC=1:2:\sqrt{3}$です。
【$x$を求める式】$AC:AB=\sqrt{3}:2より、\\\begin{align}3:x&=\sqrt{3}:2\nonumber\\\sqrt{3}x&=6\nonumber\\x&=\frac{6}{\sqrt{3}}=2\sqrt{3}\tag{答}\end{align}$
【$y$を求める式。】$AC:BC=\sqrt{3}:1より、\\\begin{align}3:y&=\sqrt{3}:1\nonumber\\\sqrt{3}y&=3\nonumber\\y&=\frac{3}{\sqrt{3}}=\sqrt{3}\tag{答}\end{align}$
このやり方は比例式とよばれるものです。普通は、この比例式を利用します。しかし、比例式が苦手という人もいるので、その場合は、下記の方法を試してみてください。
比を文字式で表す。
比を文字式にして利用する方法を紹介します。例えば、A:B=1:2というのは、Aを元にBを見ると、BはAの2倍(Bは2A)という意味で、次のように表すことができます。A:B=1A:2A。さらに、一般化して、元になる値を適当な文字t(なんでもよいです。今回はtとします。)で表すとA:B=1t:2tとなります。
辺の比を文字式として表して利用する。
辺の比は、$BC:AB:AC=1:2:\sqrt{3}$なので、これを、$BC:AB:AC=1t:2t:\sqrt{3}t$と表してみます。文字$t$はどんな文字でもよいです。自分で、分かりやすい文字にしておきます。
図2のように表せます。
- 図2:各辺の比をtの文字式として表しています。
$ABはx=2t、BCはy=1t、ACは\sqrt{3}t=3と表せます。$
したがって、
$\sqrt{3}t=3より、\\\begin{align}t&=\frac{3}{\sqrt{3}}\nonumber\\t&=\color{red}{\sqrt{3}}\nonumber\end{align}$
となります。
次に、この$t = \sqrt{3} $の値を利用して、$x$と$y$を求めます。
\begin{align} x&=2tより、x=2 \times \sqrt{3}=2\sqrt{3} \tag*{$ x=\color{red}{2 \sqrt{3}}$} \\ y&=1tより、y=1 \times \sqrt{3}= \sqrt{3} \tag*{$ y= \color{red}{\sqrt{3}} $} \end{align}
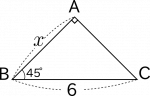
<例2>下図(図3)の直角三角形で、$x$の長さを求めなさい。
- 図3-1:45゜の直角三角形です。1:1:ルート2が使えます。BC=6のとき、xの値を求めます。
- 図3-2:1:ルート2なので1t:ルート2tとなる。
45゜の直角三角形です。つまり、直角二等辺三角形です。辺の比は、$1:1:\sqrt{2}$です。ここで、文字tを利用して、$1t:1t:\sqrt{2}t$と書き換えてみます。図3-2が実際の図形の中に辺の比を文字式として書き込んだものです。
図3-2から、$\sqrt{2}t = 6$を使って、$t$の値を求めます。
\begin{align} \sqrt{2}t &= 6 \nonumber\\ t &= \frac{6}{\sqrt{2}} \nonumber \\ t & = \color{red}{3\sqrt{2}} \nonumber\end{align}
$x = 1t $なので、
$x = 1 \times 3\sqrt{2} = \color{red}{3\sqrt{2}}$
となります。
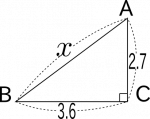
<例3>下図(図4)で、$x$の値を求めなさい。
- 図4-1:2.7と3.6が3:4:5のどれかの比に当てはまることを確認します。
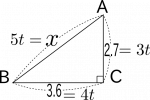
- 図4-2:3:4:5となるので、3t:4t:5tとする。
図4-1で、2.7と3.6が3:4:5のうちのどれかの比にあてはまることを確認します。(ここで、なぜ、いきなり3:4:5という比が出てきたかはあまり考えません。おそらく、辺の比が何か手がかりになるのだろうと予測していると思ってください。)
\begin{align} \color{blue}{2.7} &: \color{red}{3.6} \nonumber \\ 27 &: 36 \nonumber \\ \color{blue}{3} &: \color{red}{4} \nonumber\end{align}
したがって、2.7が3、3.6が4となります。$2.7 = 3t$、$3.6 = 4t$として、どちらかの式を利用して$t$を求めます。ここでは、$3t = 2.7$を用いて$t$を求めます。
\begin{align} 3t &= 2.7 \nonumber\\ t &= \color{red}{0.9} \nonumber \end{align}
$5t = x$に$t = 0.9$を代入し、$5 \times 0.9 = x$、$x = \color{red}{4.5}$となります。
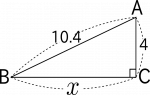
<例4>下図(図5)の$x$の値を求めなさい。
- 図5-1:10.4と4の比を簡単な比になおしてみます。そこから、手がかりを探(さぐ)ってみます。
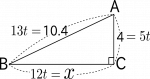
- 図5-2:5:12:13であることがわかったので、元になる値をtとして、5t:12t:13tとします。
例3と同様に、比を簡単にして、どんな比になっているのかを予測してみましょう。
\begin{align} \color{blue}{10.4} &: \color{red}{4} \nonumber \\ \color{blue}{104} &: \color{red}{40 }\nonumber \\ \color{blue}{13} &: \color{red}{5} \nonumber\end{align}
おっっ!13:5となった。これは、明らかに5:12:13ではありませんか。さっそく、5t:12t:13t(図5-2)としてみます。
図5-2から、4=5tを使って、tの値を求めます。
\begin{align} 5t &=4 \nonumber \\ t &=\frac{4}{5}= \color{red}{0.8} \nonumber\end{align}
そして、xの値を求めます。
\begin{align} x &= 12t \nonumber \\ x &= 12 \times 0.8 = \color{red}{9.6} \nonumber\end{align}
<まとめ>
比を用いた、比例式は数学だけでなく、理科などの計算分野で多く利用されます。もちろん、高校・大学でも。
しかし、比例式は苦手だという人もかなりいます。そのときは、ぜひ、このやり方も参考にしてください。