平成28年度福岡県立高校入試の数学追加問題の大問１を解説します

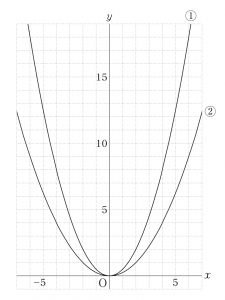
【問題１】下の図で、放物線①、放物線②の式は、それぞれ y=12x2 、y=14x2 である。1から6までの目が出るさいころを3回投げる。
1回めに出た目の数をa、2回めに出た目の数をb、3回めに出た目の数をcとし、放物線①上にx座標がaである点Aとx座標が−bである点Bをとり、放物線②上にx座標がcである点Cをとる。
次の(1)、(2)は最も簡単な数で、(3)は指示にしたがって答えよ。
ただし、根号を使う場合は の中を最も小さい整数にすること。

(1)３点Ａ、B、Cのx座標とy座標が、すべて整数になる確率を求めよ。
ただし、さいころはどの目が出ることも同様に確からしいものとする。

【前提条件】

  1. 「すべて整数になる」の意味が理解でている。
  2. 条件に合う事柄の場合の数を求めることができる。
  3. 確率を求めることができる。

＜手順＞

  1. 「すべて整数になる」の意味を理解する。
  2. 条件に合う事柄の場合の数を求める。
  3. 確率を求める。

１．「すべて整数になる」の意味を理解する。

画像１

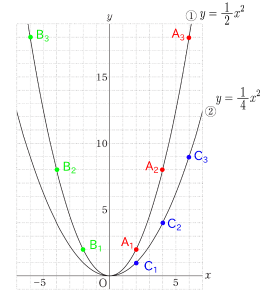
「すべて整数になる」という意味は、画像１にあるように 点A1〜点C3 を示しています。放物線①、②の比例定数が 12、14なので、x座標は偶数（さいころの目の数なので、0は含みません。）であることがわかります。

「すべて整数になる」のは、x座標が偶数であるとき。

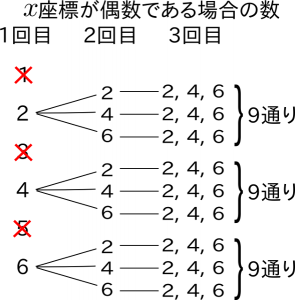
２．条件に合う事柄の場合の数を求める。

画像２

画像２にあるように、x座標が偶数である場合の数は、2、4、６（さいころなので、1から6まで）あるので、1回目、2回目、3回目より、9通り×3=27通り、または、3×3×3=27通り　です。

条件に合う事柄の場合の数は、27通り

３．確率を求める。

確率P=条件に合う事柄の場合の数(a)すべての場合の数(N)

すべての場合の数(N)=6 × 6 × 6 = 216
条件に合う事柄の場合の数(a)は、「２」より、27通り。

P=27216=18⋯（解）

次は、（２）です。


ページ: 1 2 3