(3)さいころを投げて、3回とも4の目が出た。放物線②上の $ -4 \leqq x \leqq 4 $ に対応する部分に点Pをとり、△ABPの面積が△ACPの面積の2倍になるようにする。
点Pのx座標をtとし、方程式をつくって点Pのx座標を求めよ。
解答は、解く手順にしたがってかき、答の$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$の中には、あてはまる最も簡単な数を記入せよ。
【前提条件】
- 条件に合う座標を図中に記入できる。
- 座標から、一辺の長さを求めることができる。
- 三角形の面積を求めることができる。(底辺、高さを求めることができる。)
- 二次方程式を解くことができる。
<手順>
- 条件に合う座標を図中に記入する。
- △ABPの面積を求める。
- △ACPの面積を求める。
- 二次方程式をつくり、解いて、答えを吟味する。
1.条件に合う座標を図中に記入する。
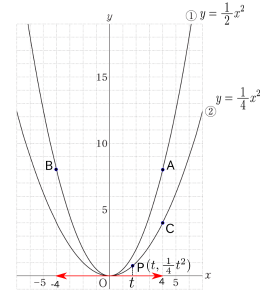
3回とも4の目が出たので、点A〜点Cのx座標はすべて4です。
各点の座標は、
点A( 4 , 8)、点B( -4 , 8 )、点C( 4 , 4 )となります。
それを、図中に記入します。
点Pは、放物線②(\( \displaystyle y = \frac{1}{\;4\;}x^{2}\))上の点で、x座標の変域は、$ -4 \leqq x \leqq 4 $なので、図中には画像4のように記入します。点Pの座標は、$\displaystyle( t , \frac{1}{\;4\;}t^{2} )$となります。
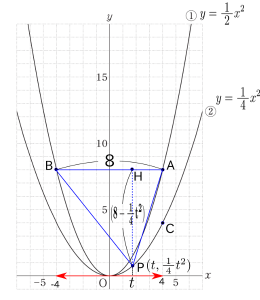
2.△ABPの面積を求める。
△ABPの面積を求めるため、底辺ABと高さPHの長さを求めます。
画像5より、$\displaystyle底辺{\rm{AB}}=8(cm)、高さ{\rm{PH}}=8 − \frac{1}{\;4\;}t^{2}(cm)$です。
\begin{align}&\rm{△ABP}の面積\nonumber\\ & = 8 × ( 8− \frac{1}{\;4\;}t^{2} ) × \frac{1}{2} \nonumber\\ & = 4 ( 8 − \frac{1}{\;4\;}t^{2} ) \nonumber\end{align}
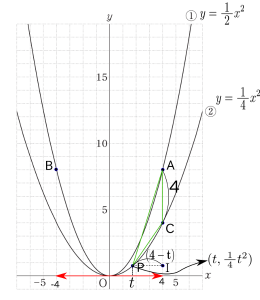
3.△ACPの面積を求める。
$\triangle \rm{ACP}$の面積を求めるために、底辺AC、高さPIの長さを求めます。
画像6より、${\rm{AC}}=4、{\rm PI}=( 4 − t)$です。
\begin{align}&\triangle {\rm ACP }の面積\nonumber\\ & = 4 \times (4 − t) \times \frac{1}{\;2\;}\nonumber\\ & = 2( 4 − t)\nonumber\end{align}
4.二次方程式をつくり、解いて、答えを吟味する。
「△ABPの面積が△ACPの面積の2倍」になるので、方程式をつくると、
$\displaystyle 4 ( 8 − \frac{1}{\;4\;}t^{2} ) = 2( 4 − t) \times 2$
になります。あとは、この二次方程式を解いて、答えを求めます。
\begin{align} 4 ( 8 − \frac{1}{\;4\;}t^{2} ) &= 2( 4 − t) \times 2\nonumber\\32 – t^{2} &= 16 – 4t\nonumber\\-t^{2} + 4t + 16 &= 0\nonumber\\t^{2} – 4t – 16 &= 0\nonumber\\[3mm]t &= \frac{4 \pm \sqrt{16 – 4 \times (-16)}}{2}\nonumber\\ & = \frac{4 \pm 4 \sqrt{5}}{2}\nonumber\\ &= 2 \pm 2\sqrt{5}\nonumber\end{align}
ここで、\(t\)の範囲は、題意より、\( -4 \leqq x \leqq 4 \)なので、\( 2 + 2\sqrt{5}\)は4より大きくなり、不適です。また、\( 2 – 2 \sqrt{5}\)は、適します。
解:$ 2 – 2 \sqrt{5} $